深層学習とアンサンブル学習をを体系的に整理したサーベイ論文 Ensemble Deep Learning: A Review の解説記事です。

この論文では、バギング・ブースティングのような古典的アンサンブル手法から、Dropout や Snapshot Ensemble といった暗黙的アンサンブル、ヘテロジニアスなモデル融合、決定融合戦略、そして応用分野までを俯瞰しています。

Introduction

まず、分類問題と回帰問題を次のような写像として定式化しておきます。

• 分類（カテゴリカル出力）

  $$O_c = h(x, \theta_c), \quad O_c \in \mathcal{Z}$$

  ここで $x$ は入力特徴量、$O_c$ はクラスラベル、$\theta_c$ は学習パラメータ、$\mathcal{Z}$ はラベル集合です。

• 回帰（連続値出力）

  $$O_r = h(x, \theta_r), \quad O_r \in \mathbb{R}$$

ネットワークモデルが $h$ で表現されています。機械学習の目的は、真の未知関数をよく近似する仮説 $h$ を得て、未知データに対する汎化誤差を下げることです。 ここで導入されるのが アンサンブル学習 です。単一の $h$ を使用するのではなく、複数モデルの予測を平均・多数決などで統合することでより良い性能を得ようというアイデアです^[1]

理論的背景

アンサンブル学習の手法が成功する理由として、論文では次のような視点を挙げています。

• 統計的・計算的・表現力に関する理由（Dietterich）
• バイアス–バリアンス分解
• strength–correlation（個々の性能と相関のトレードオフ）

一方で、深層ネットワークは非常に表現力が高い反面、勾配消失・爆発や学習の不安定さといった問題も抱えます。ResNet や Highway Network により非常に深いネットワークが実用的になりましたが、深層モデルをそのまま多数束ねる のは計算コスト的にかなり厳しいという現実もあります。 そうした制約の中で

• どうやって多様性を確保するか
• どうやって訓練コスト・モデル規模を抑えるか
• どうやって複数モデルの出力を賢く融合するか

といった課題が存在しています。

バイアス-バリアンス分解

データセットが固定で $M$ 個のモデルを学習し、それらの予測値を単純に平均を取るアンサンブルを取る場合を考えます。アンサンブルとしての出力は次のように書けます。

ここで、入力: $x$、真のターゲット（ラベル）: $t$、ベースモデル（個々のニューラルネットなど）の出力: $o_i(x)$, $i = 1,\dots,M$ です。 1 サンプル $(x,t)$ に対する二乗損失は

です。しかし、$x$ や $t$、さらには学習データや初期値などは確率的に変動します。そこで論文では、真の分布（＋学習のランダム性）に関する 期待二乗誤差

を考えます。期待値 $\mathbb{E}[o]$ を使って展開すると

となります。第 2 項は $\mathbb{E}[o]$ は定数であること（期待値計算をしているので確率変数ではない）、同様に $t$ も定数であることを利用すると

となります。第三項は、$(\mathbb{E}[o] - t)^2$ が単なる定数であることを利用して、

と書けます。よって全体は

という形になります。あとでまとめますが、$\mathbb{E}\big[(o - \mathbb{E}[o])^2\big]$ はアンサンブル出力に関する分散（バリアンス）、$(\mathbb{E}[o] -t)^2$ はバイアスです。

分散について着目します。

次に、和の二乗を展開します。一般に

なので、ここでは $a_i = (o_i - \mathbb{E}[o_i])$ とおけば、

となります。これを期待値の中に戻すと、

期待値は線形なので、和の外に出せます。

ここで出てきている期待値は、ベースモデルの分散と共分散そのものです。 各ベースモデルの分散と、ペアの共分散は

• 分散

  $$\text{Var}[o_i] = \mathbb{E}\big[(o_i - \mathbb{E}[o_i])^2\big]$$

• 共分散

  $$\text{Cov}(o_i, o_j) = \mathbb{E}\big[(o_i - \mathbb{E}[o_i])(o_j - \mathbb{E}[o_j])\big]$$

と定義されます^[2]。これを用いると、先ほどの式は

と書き換えられます。ここで、アンサンブル出力$o$ ではなく個々のベースモデル $o_i$ に関して分散、共分散を取ることを考えます。先程の式を変形すると、

と書き直すことができます。平均の計算をするために係数を無理やり作り出していることに注意してください。

さて、少し議論が長くなってしまいましたが、もともと二乗誤差について

という分解をしていました。ここに先程求めた

を代入すると、

という、アンサンブル誤差の「バイアス＋分散＋共分散」分解が得られます。ここで、

• アンサンブルのバイアス（二乗）

  $$\text{bias}^2 = (\mathbb{E}[o] - t)^2$$

• 個々のベースモデルの分散の平均

  $$\text{var} =\frac{1}{M} \sum_{i=1}^M \text{V}[o_i]$$

• 個々のベースモデル間の共分散の平均

  $$\text{covar} = \frac{1}{M(M-1)} \sum_{i=1}^M \sum_{\substack{j=1 \\ j \neq i}}^M \mathbb{E}\big[(o_i - \mathbb{E}[o_i])(o_j - \mathbb{E}[o_j])\big]$$

です。

アンサンブル手法とは何なのか？

バイアスとは、（アンサンブルによる）モデルの予測値の平均値 $\mathbb{E}[o]$ が真値からどれくらいズレているかを表す量です^[3]。バリアンスとは、データセットや初期値による予測値のブレを表す量です。どちらも小さい値であるほうが好ましい量です。その理解をしたうえで、先程導出した式

の定義を眺めると次のことが言えます。

• バイアス $\text{bias}^2$ は$M$（モデル数） に依存しない

  • ベースモデルを何個足しても、アンサンブル自体はバイアスを減らしてくれない
  • バイアスを小さくしたいなら、「1 個 1 個のモデルを強くする」必要がある

• $\dfrac{1}{M}\,\text{var}$ は $M$ を増やすと $1/M$ で減少

  • ベースモデルの「ランダムな揺らぎ」は、平均を取ることで縮小される
  • これが「アンサンブルは分散を下げる」という典型的な効果

• $\Bigl(1 - \dfrac{1}{M}\Bigr)\text{covar}$ は$M \to \infty$ のとき $\text{covar}$ に収束して残る

  • モデル同士が似たような誤差を出していると、その「共通のズレ」は平均しても消えない。

モデル数を増やすとどうなるか？

式のうち、モデル数 $M$ に依存するのは

の部分です。

$M=1$ のとき

なので

単一モデルのバイアス＋分散に一致します。

$M \to \infty$ のとき

なので

となります。つまり

• モデル数 $M$ を増やすほど、アンサンブルを構成しているモデルの予測のブレ（$\text{var}$）の寄与は小さくなる
• しかし最終的には、$\text{bias}^2 + \text{covar}$ という「下限」に近づくだけ
  • 共分散 $\text{covar}$ が大きいと、そのぶん「頭打ち」が高くなる

ということが分かります。この式が教えているのは、

• 弱くて似たモデルをたくさん並べても、あまり得をしない

  • bias が大きく、covar も大きいので、$M$ を増やしても誤差下限が高いまま

• 強くて似たモデルをたくさん並べると

  • 単体でもそこそこ良いが、「似すぎている」と covar が支配してしまい、分散低減が頭打ちになる

• 強くて多様なモデルを揃えられると

  • bias, var, covar のすべてが小さくなり、アンサンブルの恩恵が最大化される

ということです。

そのため、アンサンブルは基本的に「分散（var）」を減らす仕組みである（何も考えずモデルを複数アンサンブルするだけで精度が上がるものではない）と捉えることができます。アンサンブルによってバイアスは減らすことができず、共通の誤差（covar）が大きいと、分散低減効果が頭打ちになることも分かります。

各アンサンブル手法が狙っているもの

この式を頭に置くと、典型的な手法の意図を「var / covar の制御」として眺められます。

• Bagging / Random Forest

  • ブートストラップサンプリングや特徴サブサンプリングで
    「各モデルを少しずつ違うデータ・特徴で学習させる」
  • → var を下げつつ、covar もある程度下げる狙い

• Boosting

  • 連続的にモデルを追加し、前のモデルが苦手だった点を補正する
  • → 主に バイアスを下げる 方向の手法だが、同時に誤りパターンを変えることで covar にも影響

• Dropout / Stochastic Depth などの暗黙的アンサンブル

  • 1 つのネットワーク内部に多数のサブネットを「重ね合わせる」
  • → var を抑えつつ、サブネット間の相関（covar）も下げようとする

• Negative Correlation Learning

  • 共分散（相関）に直接ペナルティを入れて学習する
  • → 明示的に covar を小さくする ことを目的にしたアプローチ

すべて「var」と「covar」をどうコントロールするか、という観点で統一的に理解できます。

Statistical / Computational / Representational な観点

Dietterich による「アンサンブル成功の三つの理由」が整理されています。

1. Statistical（統計的）
   データ量に対して仮説空間が巨大なとき、訓練データ上はほぼ同じ性能を持つ複数の仮説が存在します。アンサンブルでそれらを平均すると、「たまたま悪い仮説を引いてしまうリスク」を下げられます。

2. Computational（計算的）
   局所探索ベースの学習アルゴリズム（例: ランダム初期化＋勾配法）は局所最適に陥りやすいです。異なる初期値やサンプリングで複数モデルを学習し、それらを統合することで、真の関数により近い近似が期待できます。

3. Representational（表現的）
   単一モデルの仮説空間には真の関数が含まれていないかもしれませんが、「複数モデルの線形結合」として見れば、より広い関数クラスを表現できます。

深層学習の文脈では、巨大なパラメータ空間や非凸最適化の難しさを考えると、どの理由もそのまま当てはまり、アンサンブルが有効であることの理論的裏付けになっています。

Ensemble Strategies

論文では、深層アンサンブル戦略を大きく

• 古典的手法（bagging, boosting, stacking）
• 一般的手法（negative correlation learning, explicit/implicit, homogeneous/heterogeneous）
• 決定融合戦略（多数決・平均・Bayes optimal classifier・stacked generalization など）

に分類しています。

Bagging

Bagging（Bootstrap Aggregating）は、最も基本的なアンサンブル戦略のひとつです。アルゴリズムは非常に素直で、次のようになります。

1. ブートストラップサンプリングで、元データからサイズ同じのサンプル集合 $D_1, \dots, D_M$ を生成する
2. 各サンプル集合ごとにベースモデル $C_1, \dots, C_M$ を独立に学習する
3. 予測時には、分類なら多数決、回帰なら平均などで出力を集約する

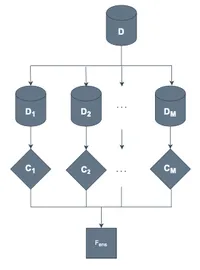
ランダムフォレストは、決定木をベースモデルとする Bagging を特徴量サブサンプリングと組み合わせたバリエーションで、木間の相関をさらに下げることで性能を上げています。Bagging 自体は計算コストが高くなる傾向があるため、subbagging や half-subbagging など計算量を抑えた変種も提案されています。

ニューラルネットに対しても、複数の MLP や自己符号化器を bagging する研究があり、個々のネットワークより良い汎化性能が得られることが示されています。ただし、深層 CNN をそのまま多数 bagging するのは現実的ではないため、実務では以下のような設計が一般的です。

• 単一ネットワークを訓練しつつ暗黙的にアンサンブル効果を得る（Dropout など）
• モデル数を少なめ（例: 3〜5）に抑えつつ、初期値やデータ拡張で多様性を確保する

Boosting

Boosting は、弱学習器を逐次的に追加しながら重み付きの線形結合で強学習器を構成する枠組みです。典型例は AdaBoost と Gradient Boosting で、それぞれ指数損失や一般的な微分可能損失を最小化します。

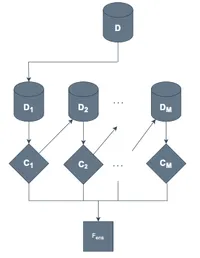
論文では、Boosting が深層モデルに取り込まれている例として、次のようなものが紹介されています。

• Boosted Deep Belief Network (DBN)
• Deep Boosting（深い決定木の集合）
• Incremental Boosting CNN (IBCNN)
• Boosted CNN / Stagewise boosting deep CNN
• 画像復元・ノイズ除去における Deep Boosting 系

さらに、

• ResNet を Boosting の観点から解析した BoostResNet
• AdaNet のような、アーキテクチャ探索と Boosting を組み合わせた枠組み

などを通じて、「残差ブロックを順に積み上げていく構造自体が、Boosting 的な逐次加法モデリングと解釈できる」という視点も示されています。

深層系の Boosting は、訓練コストの増大がボトルネックになりがちで、それを緩和するために Deep Incremental Boosting や Snapshot Boosting のような、既存モデルをうまく再利用する手法もまとめられています。

Stacking

Stacking（stacked generalization）は、複数のベースモデルの出力を入力としてメタ学習器を訓練し、最終予測を行う手法です。メタ学習器が線形モデルなら「ブレンディング」と呼ばれることもあります。

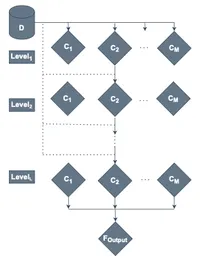
論文では、Stacking の思想を取り入れた深層アーキテクチャとして、次のような系列がまとめられています。

• Deep Convex Network (DCN)
• Deep Stacking Network (DSN) / Kernel Deep Convex Network (K-DCN)
• Tensor DSN, Sparse DSN, Group-Sparse DSN
• Recurrent DSN（R-DSN）
• Stacked Extreme Learning Machine
• Deep Forest（ランダムフォレストをスタックした深層構造）

これらは「モジュールを積み重ねることで深さを構成し、それぞれのモジュールを比較的簡単な目的関数で訓練する」という設計になっており、通常の end-to-end 深層ネットとは違うトレードオフ（並列性・解釈性など）を持ちます。

Negative Correlation Based Deep Ensemble Methods

Negative Correlation Learning (NCL) は、アンサンブル内の個々のモデルが互いに相関しないようにペナルティを入れて学習する枠組みです。

損失関数に「他モデルとの誤差相関」を加えることで、多様性を明示的に制御します。単純平均だけに頼るより、バイアス・バリアンス・共分散のバランスを直接調整できる点が利点です。

深層版としては、

• D-ConvNet（群集カウント用の Decorrelated ConvNet）
• Robust regression via deep NCL
• Generalized NCL (GNCL)：様々な既存手法を包含する一般枠組み

などが紹介されています。

Explicit / Implicit Ensembles

深層モデルのアンサンブルは、単純に「複数ネットワークを独立訓練」すると計算コストが爆発します。そこで論文は、単一のネットワークからアンサンブル効果を引き出す 手法を

• Implicit ensemble（暗黙的アンサンブル）
• Explicit ensemble（明示的アンサンブル）

に分けて整理しています。

暗黙的アンサンブルの例

• Dropout：訓練時にユニットをランダムに落とし、テスト時にはフルネットワークでスケーリングして推論する
• DropConnect：ユニットではなく「接続（重み）」をランダムに落とす
• Stochastic Depth：ResNet のブロックを訓練時にランダムスキップする
• Swapout：Dropout と Stochastic Depth の一般化
• Gradual DropIn：浅いネットから徐々に層を追加しつつ訓練する

これらは、「多数のサブネットを共有重みで訓練し、テスト時に平均化したような振る舞い」を実現します。

明示的アンサンブルの例

• Snapshot Ensemble：1 回の訓練中に複数の局所最適点で重みをスナップショットし、それらを明示的に平均化する
• Random Vector Functional Link Network の階層構造を使って多様な初期化を生成する手法 など

暗黙的・明示的アンサンブルはいずれも「単一の訓練プロセスから複数の仮想モデルを取り出す」ことで、コストを抑えつつアンサンブル効果を得ようとするアプローチになっています。

Homogeneous & Heterogeneous Ensembles

ここでは、ベースモデルの「種類」に着目して

• Homogeneous Ensemble (HOE): 同一アルゴリズムを複数個束ねる
• Heterogeneous Ensemble (HEE): 異種アルゴリズム（CNN, SVM, XGBoost など）を組み合わせる

という分類を行います。

HOE では、ランダムサンプリングや特徴サブスペース法、初期値の違いなどで多様性を稼ぎます。ランダムフォレストは典型例です。 一方、深層学習の世界では、モデルをたくさん並列学習するのは依然として負荷が高いため、

• 横方向・縦方向の voting（Horizontal / Vertical Ensemble）
• Temporal Ensemble（異なるエポックでの重みを利用）
• CNN と従来モデル（XGBoost, ロジスティック回帰など）を組み合わせた HEE

といった工夫が紹介されています。

HEE の例としては、デフォルト予測・テキスト分類・特徴選択・インクリメンタル学習・概念ドリフト対応など、多くの応用が挙げられています。

Decision Fusion Strategies

最後に、複数モデルの出力をどう統合するか という観点で整理されています。

主な戦略として、次のようなものがあります。

1. Unweighted Model Averaging（単純平均）

   • 最もよく用いられる方法です。各モデルの出力（もしくは softmax 後の確率）を平均します。
   • 深層モデルは「高バリアンス・低バイアス」な傾向があるため、平均化によるバリアンス低減が効きやすいと考えられます。

2. Majority Voting（多数決）

   • 出力ラベルの票数で決定します。弱学習器の過信やオーバーコンフィデンスなモデルに対して、単純平均より頑健な場合がありますが、類似モデルが多いとその偏りがそのまま出る問題もあります。

3. Bayes Optimal Classifier / Super Learner

   • ナイーブな平均や多数決はデータ適応的ではないため、ベイズ的に最適な重み付けや、メタ学習ベースで重み付けするアプローチが紹介されています。

4. Stacked Generalization / Consensus / Query-by-Committee

   • メタ学習器で出力を統合したり、アクティブラーニングにおける「委員会の不一致度」をクエリ戦略に用いたりと、より高度な融合方法も存在します。

脚注

1. 論文では、マルキ・ド・コンドルセの定理を引用し、「各投票者（モデル）が独立で、正解する確率が 0.5 より大きければ、人数（モデル数）を増やすほど多数決が正しい確率は 1 に近づく」という直感的な説明を紹介しています。 ↩︎
2. アンサンブルとしての出力 $o$ ではなく、個々のモデル $o_i$ に関する計算であることに注意。 ↩︎
3. バイアス自体はモデルの予測値と真値のズレを表す統計用語で、アンサンブルとは独立した概念です。 ↩︎