価値関数

強化学習において価値関数（value function）は、状態もしくは状態−行動ペアの関数で、その状態もしくは状態-行動がどれだけ「良い」かを推定するための関数です。強化学習における「良さ」とは、将来的に受け取れる報酬（期待収益; expected return）によって定義されます。

状態価値関数

方策 $\pi$ とは、各状態 $s \in \mathcal{S}$ と行動 $a \in \mathcal{A}(s)$ に対して、その状態 $s$ で行動 $a$ を選ぶ確率 $\pi(a|s)$ を与える写像であることを思い出してください。方策 $\pi$ の下での状態価値関数 $v_\pi(s)$ は、状態 $s$ から開始し、その後は $\pi$ に従うときの期待収益として次のように定義されます。

v_{\pi}(s)=\mathbb{E}_{\pi}\!\left[G_t \mid S_t=s\right] =\mathbb{E}_{\pi}\!\left[\sum_{k=0}^{\infty}\gamma^{k}R_{t+k+1}\ \middle|\ S_t=s\right]

ここで $\mathbb{E}\pi[\cdot]$ は、エージェントが方策 $\pi$ に従うという条件の下での確率変数の期待値を表し、 $t$ は任意の時刻です。

行動価値関数

方策 $\pi$ の下で状態 $s$ において行動 $a$ を取ることの価値 $q_\pi(s,a)$ を、状態 $s$ から開始し、行動 $a$ を取り、その後は方策 $\pi$ に従うときの期待収益として定義します

q_{\pi}(s,a)=\mathbb{E}_{\pi}\!\left[G_t \mid S_t=s,\ A_t=a\right] =\mathbb{E}_{\pi}\!\left[\sum_{k=0}^{\infty}\gamma^{k}R_{t+k+1}\ \middle|\ S_t=s,\ A_t=a\right].

関数 $q_\pi$ を、方策 $\pi$ の行動価値関数（action-value function）と呼びます。

ベルマン方程式

準備（広義の遷移確率）

状態の遷移確率を次のように、状態と報酬との同時確率で定義します。

p(s',r|s,a)

教科書によっては遷移確率を $p(s'|s,a)$ として定義していますが、以下では $r$ が含まれていることの説明をしておきます。一般的には、同じ $s,a,s'$ に対しての報酬

r(s,a,s')

は確率的にブレる状況が生じます。例えば測定誤差や乱数ノイズなどが生じるケースや、その瞬間の市場価格・需要・天候などで利益（報酬）が変わる様な在庫補充、電力取引、配車であったりなどのケースが挙げられます。そのため、以下のように $s'$ だけでなく $r$ も含んだ 同時確率 の形式で定義しておきます。

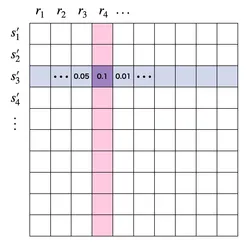図の説明 — 同じ状態に対して得られる報酬が確率的にブレる場合、同時確率として表すことになる。

状態価値関数に対する導出

価値関数の基本的な性質は、特定の再帰関係を満たすことです。任意の方策 $\pi$ と任意の状態 $s$ に対して、次の条件が成り立ちます。

\begin{aligned} v_{\pi}(s) &= \mathbb{E}_{\pi}\!\left[ G_t \mid S_t = s \right] \\ &= \mathbb{E}_{\pi}\!\left[ \sum_{k=0}^{\infty} \gamma^{k} R_{t+k+1} \ \middle|\ S_t = s \right] \\ &= \mathbb{E}_{\pi}\!\left[ R_{t+1} + \gamma \sum_{k=0}^{\infty} \gamma^{k} R_{t+k+2} \ \middle|\ S_t = s \right] \\ &= \mathbb{E}_{\pi}\!\left[ R_{t+1} \middle| S_t =s \right] + \mathbb{E}_{\pi} \left[\gamma \sum_{k=0}^{\infty} \gamma^{k} R_{t+k+2} \ \middle|\ S_t = s \right] \end{aligned}

ここで1ステップ遷移あとの状態を $S_{t+1} = s'$ とすると、方策 $\pi$ による行動の選択と遷移確率とを考慮すると第一項は

\begin{aligned} \mathbb{E}_{\pi}\!\left[ R_{t+1} \middle| S_t =s \right] &= \sum_{a} \sum_{s',r} \left( \pi(a|s) p(s',r|s,a) \times r \right)\\ \end{aligned}

と期待値の計算を行うことができます。第二項の計算も、1ステップ進めたあとの期待値に直すと

\begin{aligned} \mathbb{E}_{\pi}\!\left[ R_{t+1} \middle| S_t =s \right] &= \sum_{a} \sum_{s',r} \left( \pi(a|s) p(s',r|s,a) \times \mathbb{E}_{\pi} \left[\gamma \sum_{k=0}^{\infty} \gamma^{k} R_{t+k+2} \ \middle|\ S_{t+1} = s' \right] \right)\\ &= \sum_{a} \sum_{s',r} \left( \pi(a|s) p(s',r|s,a) \times v_\pi(s') \right)\\ \end{aligned}

と計算できます。これらを合わせると

\begin{aligned} v_{\pi}(s) &= \sum_{a} \pi(a \mid s)\, \sum_{s',r} p(s',r \mid s,a)\left[\, r + \gamma v_{\pi}(s') \right] \end{aligned}

として再帰的な関係式を導出することができます。この関係式が、価値関数 $v_\pi$ に対するベルマン方程式（Bellman equation）です。

行動価値関数に対する導出

行動価値関数 $q_\pi(s,a)$ に対してもベルマン方程式を導出できます。

\begin{aligned} q_{\pi}(s,a) &= \mathbb{E}_{\pi}\!\left[ G_t \mid S_t=s,\ A_t=a \right] \\ &= \mathbb{E}_{\pi}\!\left[ \sum_{k=0}^{\infty}\gamma^k R_{t+k+1}\ \middle|\ S_t=s,\ A_t=a \right] \\ &= \mathbb{E}_{\pi}\!\left[ R_{t+1} + \gamma \sum_{k=0}^{\infty}\gamma^k R_{t+k+2}\ \middle|\ S_t=s,\ A_t=a \right] \\ &= \mathbb{E}_{\pi}\!\left[ R_{t+1} \mid S_t=s,\ A_t=a \right] + \gamma\,\mathbb{E}_{\pi}\!\left[ \sum_{k=0}^{\infty}\gamma^k R_{t+k+2}\ \middle|\ S_t=s,\ A_t=a \right] \end{aligned}

第一項は

\begin{aligned} \mathbb{E}_{\pi}\!\left[ R_{t+1} \mid S_t=s,\ A_t=a \right] &= \sum_{s',r} p(s',r\mid s,a)\, r \end{aligned}

と書けます。第二項も同様に、

\begin{aligned} \mathbb{E}_{\pi}\!\left[ \sum_{k=0}^{\infty}\gamma^k R_{t+k+2}\ \middle|\ S_t=s,\ A_t=a \right] &= \sum_{s',r} p(s',r\mid s,a)\; \mathbb{E}_{\pi}\!\left[ \sum_{k=0}^{\infty}\gamma^k R_{t+k+2}\ \middle|\ S_{t+1}=s',\ R_{t+1}=r,\ S_t=s,\ A_t=a \right] \\ &= \sum_{s',r} p(s',r\mid s,a)\; \mathbb{E}_{\pi}\!\left[ \sum_{k=0}^{\infty}\gamma^k R_{t+k+2}\ \middle|\ S_{t+1}=s' \right] \\ &= \sum_{s',r} p(s',r\mid s,a)\; \mathbb{E}_{\pi}\!\left[ G_{t+1}\ \middle|\ S_{t+1}=s' \right] \\ &= \sum_{s',r} p(s',r\mid s,a)\; v_{\pi}(s') \end{aligned}

と書けます。これらを合わせることで、

\begin{aligned} q_{\pi}(s,a) &= \sum_{s',r} p(s',r\mid s,a)\left[ r + \gamma v_{\pi}(s') \right] \end{aligned}

と、状態価値関数に対するベルマン方程式を導出することができました。